| Angelika Langer - Training & Consulting |
| HOME | |

|
|

|
|

OVERVIEW
BY COLUMN
BY MAGAZINE
|
|
| GENERICS | |
| LAMBDAS | |
| IOSTREAMS | |
| ABOUT | |
| CONTACT |
Are Set Iterators Mutable or Immutable?
Portability Issues in Using the Standard Library
C/C++ Users Journal, October 2000
Klaus Kreft & Angelika Langer
![]()
In this column, we look into implementations of the Standard library container set , how these implementations vary, and how the differences affect the portability of our applications. In brief:
- The set container in the Standard C++ library is implemented as a binary tree, which means that the value of an element contained in a set determines its position in the internal tree structure. Like all containers in the Standard library, the set container gives access to its contained elements via iterators. Iterators are designed to give read and write access to the element they refer to by means of the dereference operator. In other words, we can modify elements in a container via the container iterators.
- In a set container, the modification of a contained element can result in corruption of the underlying tree structure [1] . Consequently, set iterators that give write access (so-called mutable iterators) are considered dangerous. Even more so since iterators are passed to algorithms and for certain algorithms (including the remove algorithms), it is not at all obvious that they corrupt a set container.
- Some library implementers try to address the problem by not providing mutable set iterators in the first place. This is safe, but comes at the cost of major restrictions on the usability of the set container. For this reason, other implementers decide to trust the user, and they provide mutable set iterators. The net effect is that there are different implementations of the set container and its iterators available, so we must keep an eye on portability issues.
The Underlying Tree Structure
The set container provided by the C++ Standard library is internally organized as a binary tree structure because the Standard defines certain complexity guarantees for all algorithms and container operations. For the set container, it requires that access to an element contained in a set must be performed in logarithmic time. In order to meet this requirement, the implementation of the set container must be based on a binary tree structure. (Details on binary tree structures can be found in every computer science book on data structures and algorithms [4] .)
Elements in a binary tree are arranged in a way that their position in the tree is determined by a sorting order. This is visible in the set container: it needs a comparator that represents an ordering on the element type. Let us consider an example. Assume we have a bank account class. It has an account number and a balance. In our application, we maintain all the bank accounts in a set container. The sorting criteria is the account number. The set uses the less-than operator defined for the element type account as a comparator, and there is an corresponding version of operator< defined that compares account objects by comparing their account numbers.
class account {
...
size_t _number; // determines ordering
double _balance; // irrelevant for ordering
};
bool operator<(const account& lhs,
const account& rhs)
{ return lhs._number < rhs._number; }
set<account> allAccounts;
The
set
uses the ordering to determine an element’s position in
the underlying binary tree. Whenever an element is inserted to the
set
,
it is automatically placed into the right location in the tree structure
so that the
set
elements are always maintained in sorted order.
When an element must be found, the respective search also uses the ordering
for efficient navigation through the tree structure. Since all operations
performed on the
set
rely on the properly arranged binary tree,
it is essential that the tree is kept intact at all times.
Naturally, the binary tree is hidden behind the interface of the set container class, and as long as we perform modifications on a set container via member functions of the set class, we will never corrupt the underlying tree structure. However, container classes in the standard library have iterators.
The Set Iterators
Like all containers in the Standard library, the set container gives access to its contained elements by means of iterators. Iterators are pointer-like objects that can be dereferenced (via the dereference operator* ) in order to access the element they point to. There are two types of iterators: those that give read and write access (let’s call them mutable iterators) and those that give only read access (the immutable iterators). In the Standard library, the mutable iterators are of type container::iterator ; the immutable iterators are of type container::const_iterator . All container classes, including the set container, must defines these two iterator types.
If we have a mutable set iterator and dereference it, we will get write access to an element contained in a set container and can modify its content. Such a modification can be quite disastrous. Think of what we are doing here: the iterator points to a node in the binary tree. The position of the element in the tree is currently correct and reflects the element’s position in the sorted sequence of contained elements. When we change the element in a way that affects the sorting order (e.g. by modifying data members that are relevant to the comparator), then the element would have to appear in a different position regarding the sorting order. The tree structure would have to be reorganized in order to reflect the new sorting order. But that’s not what will happen. We silently modify the element without changing its position in the binary tree. The result is a corrupted tree, and the behavior of operations on a corrupted tree is entirely unpredictable.
Obviously, it is not sensible to modify
set
elements through
mutable
set
iterators. Hence the unwritten rule is:
Rule 1: Never modify elements contained in a set container in a way that breaks the sorting order.This rules applies to all modifications through iterators, pointers, and references to elements contained in the set . While this rule is plausible, it turns out that it is much harder to follow than one might think.
Replacing Set Elements
Let us revisit the example to see how easy or difficult it is to follow the rule. We maintain a set of bank accounts that is sorted by account numbers. One of the clients wants to switch to another type of account and asks for his old account to be replaced by a new one. If we have an iterator pointing to the old account object, we can implement the replacement as follows:
set<account> s; ... set<account>::iterator iter; ... *iter = *new account; // direct modification of elementThis clearly violates Rule 1. While the new account will have the same data as the old one (such as name, balance, etc.), it will most likely have a different account number. Overwriting the existing position in the tree with new content will therefore include overwriting the sorting criteria and corrupt the tree structure. In order to replace an existing element in a set with a new element, we should use the member functions insert and erase rather than performing the replacement through a set iterator. The correct approach would be:
set<account> s; ... set<account>::iterator iter; ... s.insert(iter, *new account); s.erase (iter);The insert member function places the new element at the right position in the tree structure, thus keeping the tree intact. It follows another rule:
Rule 2: Do not perform replacement of an element in a set through an iterator, pointer, or reference. Use the set operations insert and erase instead.Set Containers and Generic Algorithms
This is a relatively obvious violation of Rule 1. But often the violations are less obvious. How about the following program? In our bank application, cancelled bank accounts are not immediately eliminated for the set of all bank accounts, but stay there for a while until a garbage collector removes them. Obsolete bank accounts can be recognized by their zero balance. They can be removed all at once using the remove_if algorithm. All we need is a predicate function that determines whether the balance is zero:
bool obsolete(const account& acc)
{ return acc.balance() == 0; }
Then we apply the
remove_if
algorithm and get the job done real
quick:
set<account> s; ... // remove element if balance is less than 0 s.erase(remove_if(s.begin(),s.end(),obsolete), s.end(),s.end());Looks good at first sight, but it turns out that we corrupt the set container with this approach.
Misnomers: remove Does Not Remove
In this case, it is not so obvious why we violated Rule 1. Did we affect the sorting order in any way? From the specification of the remove_if algorithm, one might conclude that we just removed certain elements from the sorted sequence, which yields another sorted sequence. In fact, the Standard specifies the remove_if algorithm as:
template<class ForwardIterator, class Predicate> ForwardIterator remove_if(ForwardIterator first, ForwardIterator last, Predicate pred);Requires: Type T is EqualityComparable.
Effects: Eliminates all the elements referred to by iterator i in the range [first, last) for which the following corresponding conditions hold: pred(*i) != false .
Returns: The end of the resulting range.
Notes: Stable; the relative order of the elements that are not removed is the same as their relative order in the original range.
Complexity: Exactly last - first applications of the corresponding predicate.
Why then does the removal break the tree structure?
The answer is that all mutating algorithms potentially break the tree structure of a set container. This is because the generic algorithms in the Standard library access container elements via iterators, and if they are mutating algorithms, they perform the modification through container iterators. The remove_if algorithm is a mutating algorithm in this sense.
The crux it that the remove algorithms (this includes
remove
,
remove_if
,
and consorts) are frequently misunderstood. Their names are misnomers:
a remove algorithm does not remove anything. In fact, not a single element
is erased from the sequence
[3]
. Instead, all the valid
elements (those accounts that are not obsolete in our example) are copied
to the beginning of the sequence, leaving a piece of garbage at the end.
The
remove_if algorithm
returns an iterator pointing to the garbage
at the end of the sequence and we must manually remove the invalid elements
by invoking the
erase
member function of the
set
container
class.
Figure 1 below illustrates the functionality
of the
remove_if
algorithm.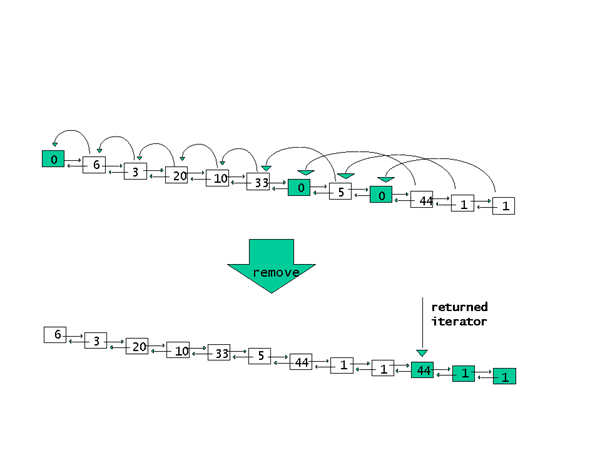
Inside the remove_if algorithm, the copying of valid elements to the beginning of the sequence is performed through iterators pointing to elements in the sequence. The algorithm does exactly what we identified as a problem under Rule 2: it assigns one element to another element through dereferenced iterators. Inside the implementation of any remove algorithm, we will find a statement such as:
*iter1 = *iter2;where iter1 and iter2 are set iterators in our case. This assignment breaks the sorting order.
Hence, it follows yet another rule for set containers:
Rule 3: Never apply a mutating algorithm to a set container.In this context, "mutating algorithms" are algorithms that modify container elements through container iterators (or references or pointers to container elements) rather than performing modification through container operations (the member function of a container). All generic algorithms in the Standard library that are mutating algorithms (such as copy , swap , replace , remove , reverse ) fall into this category.
The Dilemma
It should be clear by now that mutable set iterators are a true pitfall, because they make it easy to (inadvertently) corrupt a set container. Why then would we want to have them at all? As we will see later, it makes perfect sense that containers have mutable iterators, since we not only want to inspect elements stored in a container, but occasionally we would also want to modify those elements. Furthermore, the Standard mandates that all containers must have a mutable and an immutable iterator type. This is intrinsic to the concept of a container. Dropping the mutable iterator type for the set container would defy the idea of genericity that is central to the design of the containers and algorithms in the Standard library. As a result, library implementers are in a bind, and the Standard does not say how to escape the dilemma.
Some library implementers decide to trust their users, and with those implementations (let’s call them the relaxed implementations), it is our responsibility to make sure that we do not damage the tree structure. This, however, is often more difficult than one might think, as demonstrated above.
Other implementations aim to reduce the inherent danger and decide not to provide a mutable set iterator at all. In those implementations (let’s call them the safe implementations), the type set::iterator is a typedef for set::const_iterator . The effect is that an element stored in a set container cannot be modified through an iterator. This is obviously safer, since it at least removes the potential to corrupt the tree structure through iterators. We can still damage the set container via pointers and references to contained elements, but not providing a mutable set iterator is certainly an improvement. However, it has its price; it is kind of restrictive.
Modifying an element does not necessarily affect the sorting order. What if we just change a part of the element that is not relevant to the ordering? That would be a harmless modification. Sadly, if the set does not have a mutable set iterator, then we cannot even perform harmless modifications through an iterator, although it would be safe to do so.
Harmless Modification of Set Elements
Recall the example. We use a set of bank accounts and the sorting criteria is the account number.
class account {
...
size_t _number; // determines ordering
double _balance; // irrelevant for ordering
};
bool operator<(const account&
lhs, const account& rhs)
{ return lhs._number < rhs._number; }
set<account> allAccounts;
In this case, the balance is irrelevant for the sorting order, and it would
be safe to modify the balance data member of an account object stored in
the
set
container.
set<account>::iterator iter; ... // direct modification of part of the element iter->balance = 1000000;
In a relaxed set implementation, this will work; when using a safe set implementation, the compiler will complain about a const ness problem. No doubt, the program makes sense, but it is built on the assumption that the set iterator is mutable, which in practice is unnecessary. Hence we have a problem. The problem is mainly a portability issue [5] . What works under one implementation of the Standard library does not work under another.
How can we solve the problem?
The Brute Force Approach
Constness problems can be solved by casting away constness, right? Instead of saying
iter->balance = 1000000;we would say
*(const_cast<double*>(&(iter->_balance))) = 1000000;Note that you cannot perform a const_cast on an object, but only on pointers and references. Alternatively we could define a const member function in the account class that lets us modify the balance, but I hope we agree that casts and faked const member functions are bad programming style and should be avoided if possible. Let’s try to do better.
An Iterator Adapter
While we cannot eliminate the const_cast , we could still try to get to the core of the problem and solve it exactly where it pops up. It’s the set iterator that gets us into trouble. Why don’t we define a new iterator type that gives us access to the balance part of an account, but does not expose the account number? The idea is to adapt the set iterator so that the adapted iterator allows harmless modifications, but prohibits modification of the parts that are relevant for the sorting order.
Instead of accessing the element through a set iterator
set<account>::iterator iter; ... iter->balance = 1000000;we would access it through an adapted iterator, called balanceIter :
set<account>::iterator iter; ... *balanceIter(iter) = 1000000;In practice, C++ programmers are reluctant to implement their own user-defined iterator types because they think it is too complicated, but it is actually quite easy and very helpful. Below is the sketch of an implementation:
class balanceIter {
private:
set<account>::iterator _i;
public:
explicit balanceIter(set<account>::iterator i)
:_i(i) {}
balanceIter& operator++() { ++_i; return *this; }
// ... postfix ++, pre- and postfix -- ...
double& operator*() const
{ return *const_cast<double*>(&_i->_balance); }
};
The key points are:
- The iterator adapter stores the original iterator (the adaptee ) as a data member.
- The adaptee is provided at construction time; that is, the constructor takes the original iterator as a constructor argument.
- All typical iterator operations must be provided, such as operator++ , operator-- , operator== , and so on and so forth. They are implemented by delegation to the adaptee.
- The only interesting operation is the dereference operator. It must give write access to the balance part of the account object. Its signature differs from the signature of the adaptee’s dereference operator, because it returns a non- const reference to the balance part instead of a const reference to the entire account object.
Evaluation
We still have to do the ugly const_cast in some places, but it is now hidden in the dereference operator of the iterator adapter. There was no modification of the account class necessary and no blatant violation of const-correctness rules. And we solved exactly the problem we had encountered without opening additional safety holes. There still is an the existing safety hole; we can apply mutating algorithms to the set via the adapted iterator, but this risk is already covered by Rule 3: never apply a mutating algorithm to a set container. In addition, this solution is portable. Even when we use a relaxed set implementation, the iterator adapter would not hurt. Since all its operations are inline functions, it would not add any overhead.
In order to avoid portability problems, here is another recommendation:
Rule 4: Never modify an element contained in a set through a set iterator (of type set<T>::iterator ). Use an iterator adapter for modification of set elements that do not break the sorting order.Modifications that do not break the sorting order are changes in those parts of the contained elements that do not contribute to the sorting order.
Summary
The C++ Standard does not specify whether the iterator of a set container (type set<T>:: iterator) is a mutable or immutable iterator. As a result, popular compilers and their Standard libraries provide different implementations of the set iterator. Programs that work under one implementation might not work under another. In order to avoid portability problems, never make any assumptions regarding the (im)mutability of the set iterator.
We identified four rules that are relevant for using set containers:
Rule 1: Never modify elements contained in a set container in a way that breaks the sorting order.Rules 1 through 3 are always true independently of any particular implementation of the Standard library. Rule 4 addresses the portability issues that arise in practice due to different implementations of the set container and its iterator type.Rule 2: Do not perform replacement of an element in a set through an iterator, pointer, or reference. Use the set operations insert and erase instead.
Rule 3: Never apply to a set container an algorithm that modifies container elements through iterators, references, or pointers to container elements. This includes all mutating generic algorithms in the Standard library.
Rule 4: Never modify an element contained in a set through a set iterator (of type set<T>::iterator ). Use an iterator adapter for modification of set elements that do not break the sorting order.
| Listing 1: The balanceIterator adapter |
|
class balanceIterator { public: typedef set<account>::iterator adapted_type; typedef adapted_type::iterator_category iterator_category; typedef adapted_type::value_type value_type; typedef adapted_type::distance_type difference_type; typedef double* pointer; typedef double& reference; balanceIterator() {} explicit balanceIterator(adapted_type i) :adaptee(i) {} template <class Iter> adapted_type base() const { return adaptee; } reference operator*() const {return const_cast<reference>(adaptee->balance()); } pointer operator->() const { return &(operator*()); } balanceIterator& operator++() { ++adaptee; return (*this); } balanceIterator operator++(int) { balanceIterator _Tmp = *this; ++adaptee; return (_Tmp); } balanceIterator& operator--() { --adaptee; return (*this); } balanceIterator operator--(int) { balanceIterator _Tmp = *this; --adaptee; return (_Tmp); } private: adapted_type adaptee; }; inline bool operator==(const balanceIterator& x, const balanceIterator& y) { return x.base() == y.base(); } inline bool operator!=(const balanceIterator& x, const balanceIterator& y) { return x.base() != y.base(); } |
References
[1] Herb Sutter. "Standard Library News, Part2, Sets and Maps," C++ Report (October 1999). This article gives background information on sets and maps; Sutter explains why keys in associative arrays like set must not be modified.
[2] Cormen, Leiserson, and Rivest Introduction to Algorithms (MIT Press, 1990).
[2] Klaus Kreft and Angelika Langer. "Iterators in the Standard C++ Library, " C++ Report (November/December 1996). The article is also available at http://www.AngelikaLanger.com/Articles/IteratorsInStdlib/cppr9612_kreft.html.
[3] Matt Austern. "Algorithms and Containers," C++ Report (July/August 2000). This article also points out the problem of applying the remove algorithms to associative containers and suggests a solution using container-based generic algorithms and container traits, which are not part of the Standard.
[4] Cormen, Leiserson, and Rivest Introduction to Algorithms (MIT Press, 1990).
[5]How can one have a portability problem with the Standard
library? After all, the purpose of a standard is that it defines a portability
platform. True, it's just that in this case we are talking about an open
issue in the C++ Standard: the implementation of the
set
iterators
is still an open issue (#103) on the Standards Committee issue list. The
problem is identified and a clarification will be added to the Standard.
|
If you are interested to hear more about this and related topics you might want to check out the following seminar: |
||||
Seminar
|
||||